Max Weinreich

About me
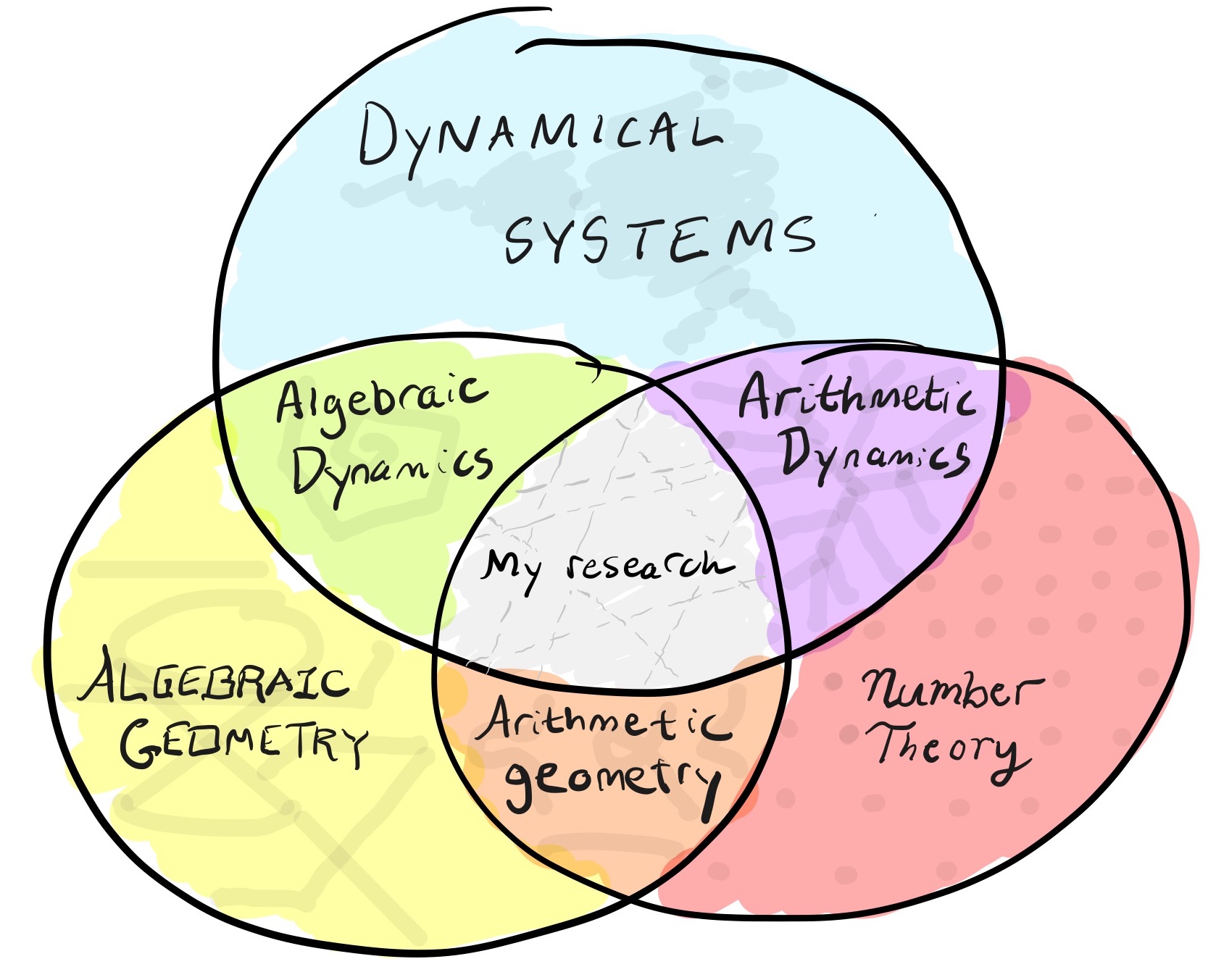
I am an NSF Postdoctoral Fellow at Harvard University, working at the intersection of dynamical systems, algebraic geometry, and number theory. I received my Ph. D. from Brown University in May 2022, advised by Joe Silverman.Pronouns: he/him
Contact Info
Email: mweinreich [at] math [dot] harvard [dot] eduAbout my math
I study arithmetic dynamics, which is the study of iteration of functions in number theory. My particular interests include billiards, moduli spaces, integrable systems, finite fields, and projective configurations.
Papers
6. The dynamical degree of billiards in an algebraic curve. 46 pages (2023). Preprint.
We introduce an algebraic formulation of billiards on plane curves over algebraically closed fields, extending Glutsyuk’s complex billiards. For any nondegenerate algebraic curve C_0 of degree d >= 2, algebraic billiards is a rational (d − 1)-to-(d − 1) surface correspondence on the space of unit cotangent vectors based on C_0. We prove that the dynamical degree of the billiards correspondence is at most an explicit cubic algebraic integer, depending only on the degree d of C_0. We also study real entropy bounds, orbit growth, singularity confinement, and the existence of an invariant 2-form.
5. GIT stability of linear maps on projective space with marked points. 32 pages (2021). Preprint.
We define a moduli space for projective linear maps with marked points. Our moduli spaces are constructed using geometric invariant theory, in the style of Mumford. We interpret the stability and semistability conditions for points in the moduli space via the polyhedral combinatorics of the full root polytope of type A_N, arising in Lie theory.
4. Dynamical moduli spaces and polynomial endomorphisms of configurations. 33 pages [with Talia Blum, John Doyle, Trevor Hyde, Colby Kelln, and Henry Talbott.] Arnold Math Journal (2021).
A portrait is a combinatorial model for a discrete dynamical system on a finite set. We study the geometry of portrait moduli spaces, whose points correspond to equivalence classes of point configurations on the affine line for which there exist polynomials realizing the dynamics of a given portrait. We present results and pose questions inspired by a large-scale computational survey of intersections of portrait moduli spaces for polynomials in low degree.
3. The algebraic dynamics of the pentagram map. 46 pages. Ergodic Theory and Dynamical Systems (2022).
The pentagram map, introduced by Schwartz in 1992, is a dynamical system on the moduli space of polygons in the projective plane. Its real and complex dynamics have been explored in detail. We study the pentagram map over an arbitrary algebraically closed field of characteristic not equal to 2. We prove that the pentagram map on twisted polygons is a discrete integrable system: it is birational to a self-map of a family of abelian varieties.
2. Automorphism groups of endomorphisms of P^1(F_p). 34 pages. [with Julia Cai and Benjamin Hutz and Leo Mayer.] Glasgow Math Journal (2022).
We study automorphisms of self-maps of the projective line over the algebraic closure of a finite field. We show that every finite subgroup of PGL(F_q) can arise as an automorphism group, and prove some bounds on the degrees. We also completely describe the automorphism loci of degree 2 maps for all characteristics.
1. Counting arcs in projective planes via Glynn's algorithm. 17 pages. [with Kaplan, N., Kimport, S., Lawrence, R., Peilen, P.] Journal of Geometry (2017).
Arcs are collections of points in linear general position, a fundamental concept in classical and algebraic geometry. We count arcs in combinatorial projective planes in terms of highly determined configurations of points and lines.
Notes
Mapping classes and character varieties